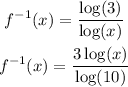Question

finding inverse of exponential functions 1.) y=3^1/x2.) y= 10^x/3how exactly do I solve these problems

Answer 1

Firts, lets switch x and y

`\begin{gathered} y=3^{(1)/(x)}\rightarrow x=3^{(1)/(y)} \\ y=10^{(x)/(3)}\rightarrow x=10^{(y)/(3)} \end{gathered}`

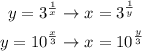
In order to find the inverse, we have to clear y.

To do this with an exponential function, we use a little trick:

Apply log to both sides:

`\begin{gathered} x=3^{(1)/(y)}\rightarrow\log (x)=\log (3^{(1)/(y)}) \\ x=10^{(y)/(3)}\rightarrow\log (x)=\log (10^{(y)/(3)}) \end{gathered}`

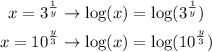
We do this in order to use the property of logarithms that allow us to turn an exponent into a coefficient.

Mathematically speaking,

`\log (x^y)=y\log (x)`

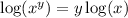
(Note: Remember that log refers to natural logarithm; a logarithm with base e)

Thus,

`\begin{gathered} \log (x)=(1)/(y)\log (3) \\ \log (x)=(y)/(3)\log (10) \end{gathered}`

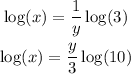
Clearing y to get the inverse,

`\begin{gathered} y=(\log (3))/(\log (x)) \\ y=(3\log (x))/(\log (10)) \end{gathered}`

Therefore,

`\begin{gathered} f^(-1)(x)=(\log (3))/(\log (x)) \\ f^(-1)(x)=(3\log (x))/(\log (10)) \end{gathered}`