Question

The data set represents the number of rings each person in a room is wearing. 0, 2, 4, 0, 2, 3, 2, 8, 6 What is the interquartile range of the data?

2
3
4
6

Answer 1

Option C.

Explanation:

The given data set is

0, 2, 4, 0, 2, 3, 2, 8, 6

Arrange the data in ascending order.

0, 0, 2, 2, 2, 3, 4, 6, 8

Divide the data set in 4 equal parts.

(0, 0), (2, 2), 2,( 3, 4), (6, 8)

Now, we get

`Q_1=(0+2)/(2)=1`

`Q_2=Median=2`

`Q_3=(4+6)/(2)=5`

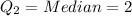
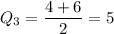
The interquartile range formula:

`IQR=Q_3-Q_1`

`IQR=5-1`

`IQR=4`

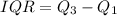
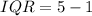
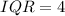
The interquartile range of the data is 4. Therefore, option C is correct.

Answer 2

d1,..,d9 = 0,0,2,2,2,3,4,6,8 //there are 9 values, in ascending order
Q2 (median) = d5 = 2 //value in the middle
Q1 = (d2+d3) / 2 = (0+2)/2 = 1
(Q1 is middle value of d1,d2,d3,d4, but there is no middle element among four elements, that is why arithmetic mean is taken)
Q3 = (d7+d8) / 2 = (4+6)/2 = 5
interquantlie range = IQR = Q3 - Q1 = 5 -1 = 4
answer: 4