Question

Use synthetic division to solve (x^4 – 1) ÷ (x – 1). What is the quotient

a. x^3-x^2+x-1
b. x^3
c.x^3+x^2+x+1
d. x^3-2

Answer 1

Hello,

x^4-1=(x²-1)(x²+1)=(x²+1)(x-1)(x+1)
==>(x^4-1)/(x-1)=(x²+1)(x+1)=x^3+x^2+x+1
Answer C

Answer 2

Option C.

Explanation:

We have to solve
`(x^(4)-1 )/(x-1)` by synthetic division and tell the quotient.

First we will write the numerator in the standard form as
`ax^(4)+bx^(3)+cx^(2)+dx+e`

Which will become as
`1.x^(4)+0.x^(3)+0.x^(2)+0.x^(1)-1`

Since denominator of the fraction is (x -1) therefore we take x = 1 as zero root.

Now we form the synthetic form as below

1 0 0 0 -1

1 1 1 1 1 0

x³ x² x

Here coefficient of x³ is 1, for x² is 1, for x is 1, and constant term 1.

Now the fraction will come in the form of

`(x -1) + ((1.x^(3)+1.x^(2)+1.x+1))/((x - 1))`

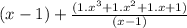
Therefore quotient will be
`x^(3)+x^(2)+x+1`

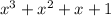
Option C. is the answer