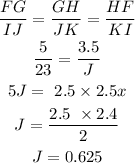The given set of traimgels FGH and IJK :
Triangles FGH and IJK are similar
From the properties of similar triangle
The ratio of the length of corrsponding sides of similar triangle are always equal
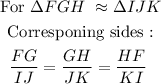
Substiute the vale :
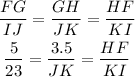
We need to find the length of JK , Simplify the
Susbstitutw thw vales and simlify :