Question

Please help me with this quickly, please make it simple and easy I don’t understand any other tutors

Answer 1

40 meters per minute

Step-by-step explanation

We have to find the rate of the wind - in other words, the speed of the wind.

We know that the duck can fly 2400 m in 10 minutes with the wind, so the speed of the duck when it is flying with the wind is,

`s_{with\text{ }the\text{ }wind}=(2400m)/(10min)=240m/min`

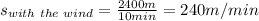
However, when the duck is flying against the wind, it can only fly 2/3 of this distance in the same time, which is,

`2400m\cdot(2)/(3)=1600m`

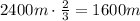
So, the speed of the duck against the wind is,

`s_{against\text{ }the\text{ }wind}=(1600m)/(10min)=160m/min`

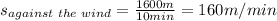
The speed of the duck with the wind is the sum of the actual speed of the duck and the speed of the wind,

`s_{with\text{ }the\text{ }wind}=s_(duck)+s_(wind)`

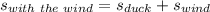
While the speed of the duck against the wind is the actual speed of the duck minus the speed of the wind,

`s_{against\text{ }the\text{ }wind}=s_(duck)-s_(wind)`

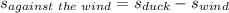
If we subtract the equation of the speed against the wind from the equation of the speed with the wind, we have,

`\begin{gathered} s_{with\text{ }the\text{ }wind}-s_{against\text{ }the\text{ }wind}=s_(duck)-s_(duck)+s_(wind)-(-s_(wind)) \\ \\ s_{with\text{ }the\text{ }wind}-s_{against\text{ }the\text{ }wind}=0+s_(wind)+s_(wind) \\ \\ s_{with\text{ }the\text{ }wind}-s_{against\text{ }the\text{ }wind}=2s_(wind) \end{gathered}`

Solving for the speed of the wind and replacing the values,

`s_(wind)=\frac{s_{with\text{ }the\text{ }wind}-s_{against\text{ }the\text{ }wind}}{2}=(240m/min-160m/min)/(2)=(80m/min)/(2)=40m/min`

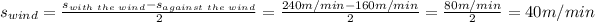
Hence, the speed (or rate) of the wind is 40 meters per minute.