Question

Find the equation of the axis of symmetry. The vertex of its graph.Graph the function.

Answer 1

we have the function

`f(x)=-2x^2-8x-3`

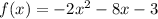
This is a vertical parabola open downward (the leading coefficient is negative)

The vertex is a maximum

The axis of symmetry is the x-coordinate of the vertex

so

Convert the given equation into vertex form

y=a(x-h)^2+k

where

(h,k) is the vertex

x=h ----> axis of symmetry

step 1

Factor -2

`f(x)=-2(x^2+4x)-3`

step 2

Complete the square

`\begin{gathered} f(x)=-2(x^2+4x+4-4)-3 \\ f(x)=-2(x^2+4x+4)-3+8 \\ f(x)=-2(x^2+4x+4)+5 \end{gathered}`

step 3

Rewrite as perfect squares

`f(x)=-2(x+2)^2+5`

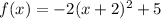
The vertex is the point (-2,5)

The axis of symmetry is x=-2

see the attached figure below