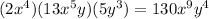Question

(2x^4)(13x^5 y)(5y^3

Answer 1

Use the laws of exponents and the commutative property of multiplications to rewrite the expression:

`(2x^4)(13x^5y)(5y^3)`

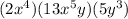
Factor out constants:

`=2\cdot13\cdot5\cdot x^4\cdot x^5\cdot y\cdot y^3`

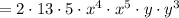
Simplify the coefficient of the expression:

`=130x^4\cdot x^5\cdot y\cdot y^3`

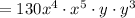
Use the fact that (a^n)(a^m)=a^(n+m) to simplify the powers of the variables x and y:

`\begin{gathered} =130x^(4+5)\cdot y^(1+3) \\ =130x^9\cdot y^4 \end{gathered}`

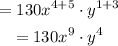
Therefore:

`(2x^4)(13x^5y)(5y^3)=130x^9y^4`