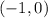In order to graph this function, let's identify the type of graph of each part, and then calculate two or more points from each part:
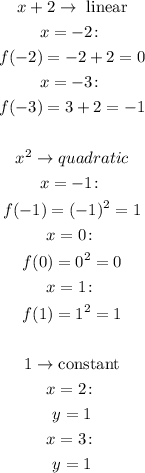
Graphing all these points and the corresponding lines or curves, we have:
Looking at the graph, we can see that the function is increasing for the interval:
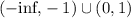
And the function is decreasing for the interval: