Question

Determine if line AB and line CD are parallel, perpendicular or neither given the coordinatesA(0, 13), B(7, 11), C(12, 10), and D(10,3). Explain why. Show all work.

Answer 1

Line AB is perpendicular to line CD.

`m_(AB)* m_(CD)=-1`

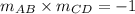
Step-by-step explanation:

For the lines to be parallel they must have the same slope.

For the lines to be perpendicular they must have negative reciprocal slopes.

Else neither of them is true.

Given the coordinates;

`A\left(0,13\right),B\left(7,11\right),C\left(12,10\right),D\left(10,3\right)`

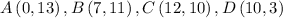
The slope can be calculated for each line as;

`m=(y_2-y_1)/(x_2-x_1)`

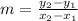
Using the formula to calculate the slope of each line;

For line AB;

`m_(AB)=(11-13)/(7-0)=(-2)/(7)`

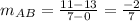
For line CD;

`m_(CD)=(3-10)/(10-12)=(-7)/(-2)=(7)/(2)`

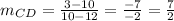
Since the slope of line AB and line CD is not the same, they are not parallel.

The slope of line AB is a negative reciprocal of the slope of line CD

`m_(AB)* m_(CD)=-1`

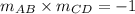
Therefore, Line AB is perpendicular to line CD.