Question

A baseball is hit with a speed of 28.0 m/s at an angle of 46.0 ∘ . It lands on the flat roof of a 12.0 m-tall nearby building.Part AIf the ball was hit when it was 1.5 m above the ground, what horizontal distance does it travel before it lands on the building?

Answer 1

We know that this is a projectile motion. which means that the horizontal and vertical position at any given time are given by the equations:

`\begin{gathered} x=x_0+(v_0\cos\theta)t \\ y=y_0+(v_0\sin\theta)t-(1)/(2)gt^2 \end{gathered}`

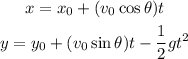
Vertically, we know that the initial height is 1.5 m, the final height is 12 m; we also know that the initial velocity is 28m/s and that is has an angle of 46° and that the acceleration of gravity is 9.8 m/s2; plugging these values in the equation for the vertical position we have:

`\begin{gathered} 12=1.5+(28\sin46)t-(1)/(2)(9.8)t^2 \\ 4.9t^2-20.14t+10.5=0 \end{gathered}`

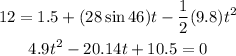
Solving for the time using the quadratic formula we have:

`\begin{gathered} t=(-(-20.14)\pm√((-20.14)^2-4(4.9)(10.5)))/(2(4.9)) \\ \text{ then} \\ t=(20.14+√((-20.14)^2-4(4.9)(10.5)))/(9.8)=3.5 \\ \text{ or} \\ t=(20.14-√((-20.14)^2-4(4.9)(10.5)))/(9.8)=0.61 \end{gathered}`

Hence, the ball will have a height of 12 m at 0.61 s or 3.5 s.

Once we know the time when the ball reaches this height we need to notice that the problem says that the ball lands on the roof, from this we can conclude that the ball is already falling when this happens and for this reason we will use the second time, that is 3.5 s.

Now that we determine this, we just need to plug the values in the expression for the x position, in here we will assume the initial position on the x direction is zero, then we have:

`\begin{gathered} x=0+(28\cos46)(3.5) \\ x=68.1 \end{gathered}`

Therefore, the horizontal distance the ball travelled is 68.1 meters