Question

Which expression represents the series 1+5+25+125+625?

Answer 1

1(5)^0 + 1(5)^1 + 1(5)^2...

The expression representing the series would be

f(x) = 5^(x-1)

Answer 2

it is a geometric sequence
an=a1(r)^(n-1)
a1=first term
r=common ratio
n=which term
first term is 1
common ratio is 5
an=1(5)^(n-1)

that is the equatin/formulf for the nth term

if you want a summation formula of the sequence to the nth term
Sn=
`(a1(1-r^(n)))/(1-r)`
in this case
Sn=
`(1(1-5^(n)))/(1-5)` or
Sn=
`(1-5^(n))/(-4)`
so in this case
up to 5th term

S5=
`(1-5^(5))/(-4)`
S5=
`(1-3125)/(-4)`
S5=
`(-3124)/(-4)`
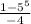
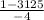
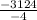
S5=781


anyway

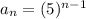
`a_(n)=(5)^(n-1)` is the nth term
and
Sn=
`(1-5^(n))/(-4)` is the summation up to the nth term