Question

Given a polynomial function f(x), describe the effects on the y-intercept, regions where the graph is increasing and decreasing, and the end behavior when the following changes are made. Make sure to account for even and odd functions.

When f(x) becomes f(x) − 3
When f(x) becomes −2 ⋅ f(x)

Answer 1

The y-intercept of is .
Of course, it is 3 less than , the y-intercept of .
Subtracting 3 does not change either the regions where the graph is increasing and decreasing, or the end behavior. It just translates the graph 3 units down.
It does not matter is the function is odd or even.

is the mirror image of stretched along the y-direction.
The y-intercept, the value of for , iswhich is times the y-intercept of .Because of the negative factor/mirror-like graph, the intervals where increases are the intervals where decreases, and vice versa.
The end behavior is similarly reversed.
If then .
If then .
If then .
The same goes for the other end, as tends to .
All of the above applies equally to any function, polynomial or not, odd, even, or neither odd not even.
Of course, if polynomial functions are understood to have a non-zero degree, never happens for a polynomial function.

Answer 2

First of all, let's review the definition of some concepts.

Even and odd functions:

A function is said to be even if its graph is symmetric with respect to the
`y-axis`, that is:

`y=f(x) \ is \ \mathbf{even} \ if, \ for \ each \ x \ in \ the \ domain \ of \ f, \\ f(-x)=f(x)`

On the other hand, a function is said to be odd if its graph is symmetric with respect to the origin, that is:

`y=f(x) \ is \ \mathbf{odd} \ if, \ for \ each \ x \ in \ the \ domain \ of \ f, \\ f(-x)=-f(x)`

Analyzing each question for each type of functions using examples of polynomial functions. Thus:

FOR EVEN FUNCTIONS:

1. When
`f(x)` becomes
`f(x)-3`

1.1 Effects on the y-intercept

We need to find out the effects on the y-intercept when shifting the function
`f(x)` into:

`f(x)-3`

We know that the graph
`f(x)` intersects the y-axis when
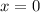`x=0`, therefore:

`y=f(0) \ is \ the \ y-intercept \ of \ f`

So:

`y=f(0)-3 \ is \ the \ new \ y-intercept`

So the y-intercept of
`f(x)-3` is three units less than the y-intercept of
`f(x)`

1.2. Effects on the regions where the graph is increasing and decreasing

Given that you are shifting the graph downward on the y-axis, there is no any effect on the intervals of the domain. The function
`f(x)-3` increases and decreases in the same intervals of
`f(x)`

1.3 The end behavior when the following changes are made.

The function is shifted three units downward, so each point of
`f(x)-3` has the same x-coordinate but the output is three units less than the output of
`f(x)`. Thus, each point will be sketched as:

`For \ y=f(x): \\ P(x_(0),f(x_(0))) \\ \\ For \ y=f(x)-3: \\ P(x_(0),f(x_(0))-3)`

FOR ODD FUNCTIONS:

2. When
`f(x)` becomes
`f(x)-3`

2.1 Effects on the y-intercept

In this case happens the same as in the previous case. The new y-intercept is three units less. So the graph is shifted three units downward again.

An example is shown in Figure 1. The graph in blue is the function:

`y=f(x)=x^3-x`

and the function in red is:

`y=f(x)-3=x^3-x-3`

This function is odd, so you can see that:

`y-intercept \ of \ f(x)=0 \\ y-intercept \ of \ f(x)-3=-3`

2.2. Effects on the regions where the graph is increasing and decreasing

The effects are the same just as in the previous case. So the new function increases and decreases in the same intervals of
`f(x)`

In Figure 1 you can see that both functions increase and decrease at the same intervals.

2.3 The end behavior when the following changes are made.

It happens the same, the output is three units less than the output of
`f(x)`. So, you can write the points just as they were written before.

So you can realize this concept by taking a point with the same x-coordinate of both graphs in Figure 1.

FOR EVEN FUNCTIONS:

3. When
`f(x)` becomes
`-2.f(x)`

3.1 Effects on the y-intercept

As we know the graph
`f(x)` intersects the y-axis when
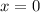`x=0`, therefore:

`y=f(0) \ is \ the \ y-intercept \ again`

And:

`y=-2f(0) \ is \ the \ new \ y-intercept`

So the new y-intercept is the negative of the previous intercept multiplied by 2.

3.2. Effects on the regions where the graph is increasing and decreasing

In the intervals when the function
`f(x)` increases, the function
`-2f(x)` decreases. On the other hand, in the intervals when the function
`f(x)` decreases, the function
`-2f(x)` increases.

3.3 The end behavior when the following changes are made.

Each point of the function
`-2f(x)` has the same x-coordinate just as the function
`f(x)` and the y-coordinate is the negative of the previous coordinate multiplied by 2, that is:

`For \ y=f(x): \\ P(x_(0),f(x_(0))) \\ \\ For \ y=-2f(x): \\ P(x_(0),-2f(x_(0)))`

FOR ODD FUNCTIONS:

4. When
`f(x)` becomes
`-2f(x)`

See example in Figure 2

`y=f(x)=x^3-x`

and the function in red is:

`y=-2f(x)=-2(x^3-x)`

4.1 Effects on the y-intercept

In this case happens the same as in the previous case. The new y-intercept is the negative of the previous intercept multiplied by 2.

4.2. Effects on the regions where the graph is increasing and decreasing

In this case it happens the same. So in the intervals when the function
`f(x)` increases, the function
`-2f(x)` decreases. On the other hand, in the intervals when the function
`f(x)` decreases, the function
`-2f(x)` increases.

4.3 The end behavior when the following changes are made.

Similarly, each point of the function
`-2f(x)` has the same x-coordinate just as the function
`f(x)` and the y-coordinate is the negative of the previous coordinate multiplied by 2.