Question

Pls the primitive of this function

Answer 1

Let F (n) denote the integral,

∫ x (1 - ln(x))ⁿ dx

We attempt to find a power-reduction formula for F (n) in terms of F (n - 1). Integrate by parts, with

u = (1 - ln(x))ⁿ → du = - n/x (1 - ln(x))ⁿ ⁻¹ dx

dv = x dx → v = 1/2 x ²

Then

F (n) = u v - ∫ v du

F (n) = 1/2 x ² (1 - ln(x))ⁿ + n/2 ∫ x (1 - ln(x))ⁿ ⁻¹ dx

F (n) = 1/2 x ² (1 - ln(x))ⁿ + n/2 F (n - 1)

From this relation, we get

F (n - 1) = 1/2 x ² (1 - ln(x))ⁿ ⁻¹ + (n - 1)/2 F (n - 2)

F (n - 2) = 1/2 x ² (1 - ln(x))ⁿ ⁻² + (n - 2)/2 F (n - 3)

F (n - 3) = 1/2 x ² (1 - ln(x))ⁿ ⁻³ + (n - 3)/2 F (n - 4)

and so on, down to

F (1) = 1/2 x ² (1 - ln(x)) + 1/2 F (0)

where

F (0) = ∫ x dx = 1/2 x ² + C

By recursively substituting, we find

→ F (n) = 1/2 x ² (1 - ln(x))ⁿ + n/2 [1/2 x ² (1 - ln(x))ⁿ ⁻¹ + (n - 1)/2 F (n - 2)]

… = 1/2 x ² (1 - ln(x))ⁿ + n/2² x ² (1 - ln(x))ⁿ ⁻¹ + (n (n - 1))/2² F (n - 2)

→ F (n) = 1/2 x ² (1 - ln(x))ⁿ + n/2² x ² (1 - ln(x))ⁿ ⁻¹ + (n (n - 1))/2² [1/2 x ² (1 - ln(x))ⁿ ⁻² + (n - 2)/2 F (n - 3)]

… = F (n) = 1/2 x ² (1 - ln(x))ⁿ + n/2² x ² (1 - ln(x))ⁿ ⁻¹ + (n (n - 1))/2³ x ² (1 - ln(x))ⁿ ⁻² + (n (n - 1) (n - 2))/2³ F (n - 3)

→ F (n) = 1/2 x ² (1 - ln(x))ⁿ + n/2² x ² (1 - ln(x))ⁿ ⁻¹ + (n (n - 1))/2³ x ² (1 - ln(x))ⁿ ⁻² + (n (n - 1) (n - 2))/2³ [1/2 x ² (1 - ln(x))ⁿ ⁻³ + (n - 3)/2 F (n - 4)]

… = 1/2 x ² (1 - ln(x))ⁿ + n/2² x ² (1 - ln(x))ⁿ ⁻¹ + (n (n - 1))/2³ x ² (1 - ln(x))ⁿ ⁻² + (n (n - 1) (n - 2))/2⁴ x ² (1 - ln(x))ⁿ ⁻³ + (n (n - 1) (n - 2) (n - 3))/2⁴ F (n - 4)

and so on, down to

F (n) = 1/2 x ² (1 - ln(x))ⁿ + n/2² x ² (1 - ln(x))ⁿ ⁻¹ + … + (n (n - 1) … 2 × 1)/2ⁿ F (0)

F (n) = 1/2 x ² (1 - ln(x))ⁿ + n/2² x ² (1 - ln(x))ⁿ ⁻¹ + … + (n (n - 1) … 2 × 1)/2ⁿ ⁺¹ x ² + C

We can write this more compactly as the sum,

`F(n)=\displaystyle\int f_n(x)\,\mathrm dx=x^2\sum_(k=0)^n (n!)/(2^(k+1) (n-k)!) (1-\ln(x))^(n-k) + C`

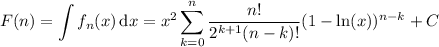
or

`F(n)=\displaystyle\int f_n(x)\,\mathrm dx=x^2\sum_(k=0)^n (k!)/(2^(k+1))\binom nk(1-\ln(x))^(n-k) + C`

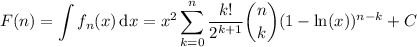
where
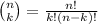`\binom nk=(n!)/(k!(n-k)!)` is the binomial coefficient.