Question

What is the length of the unknown side of the right triangle usingthe Pythagorean Theorem? Use the calculator provided and scratchpaper to show your work

Answer 1

Kindly refer to attachment!

Answer 2

The Pythagorean theorem states that the sum of the squares of the sides of a right triangle is equal to the square of the hypothenuse, you can express this theorem as follows:

`a^2+b^2=c^2`

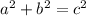
Where

a is the shortest side

b is the medium side

c is the longest side (hypothenuse)

The right triangle shown in the picture is missing the length of the hypothenuse, to calculate it you have to replace the expression above with the lengths of the sides:

a= 7

b=24

`\begin{gathered} a^2+b^2=c^2 \\ 7^2+24^2=c^2 \end{gathered}`

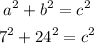
-Solve the squares and add:

`\begin{gathered} 49+576=c^2 \\ 625=c^2 \end{gathered}`

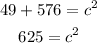
-Calculate the square root to both sides to reach the value of c:

`\begin{gathered} \sqrt[]{625}=\sqrt[]{c^2} \\ 25=c \end{gathered}`

The length of the missing side is x=25 units.