Question

The function f(t) = 4t2 − 8t + 6 shows the height from the ground f(t), in meters, of a roller coaster car at different times t. Write f(t) in the vertex form a(x − h)2 + k, where a, h, and k are integers, and interpret the vertex of f(t).

f(t) = 4(t − 1)2 + 3; the minimum height of the roller coaster is 3 meters from the ground
f(t) = 4(t − 1)2 + 3; the minimum height of the roller coaster is 1 meter from the ground
f(t) = 4(t − 1)2 + 2; the minimum height of the roller coaster is 2 meters from the ground
f(t) = 4(t − 1)2 + 2; the minimum height of the roller coaster is 1 meter from the ground

Answer 1

The correct option is 3.

Explanation:

The vertex form of a parabola is

`f(x)=a(x-h)^2+k` .... (1)

where a, h, and k are integers, and interpret the vertex of f(t). (h,k) is the vertex of the parabola.

The given function is

`f(x)=4t^2-8t+6`

It can be written as

`f(x)=4(t^2-2t)+6`

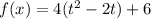
If an expression is defined as
`x^2+bx`, then we need to add
`((b)/(2))^2` to make it perfect square.

In the expression
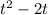`t^2-2t` the value of b is -2. So, we nned to add and subtract
`((-2)/(2))^2` in the parenthesis.

`f(x)=4(t^2-2t+1^2-1^2)+6`

`f(x)=4(t^2-2t+1)+4(-1)+6`

`f(x)=4(t-1)^2-4+6`

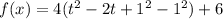
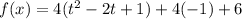
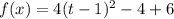
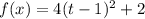`f(x)=4(t-1)^2+2` .... (2)

The vertex form of the parabola is
`f(x)=4(t-1)^2+2`.

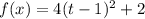From (1) and (2), we get h=1 and k=2. It means the vertex of the parabola is (1,2). Vertex of upward parabola is point of minima. So the minimum height of the roller coaster is 2 meters from the ground.

Therefore the correct option is 3.