Question

How many milliliters of 0.259 M calcium sulfate solution are needed to supply 4.45 g of calcium sulfate? Explain your process and how you got your answer.

Answer 1

We are given the molarity of the solution, the molarity corresponds to the following expression:

`\text{Molarity}=\text{ }\frac{\text{Moles of solute}}{\text{Liter of solution}}`

That is, in one liter of solution there will be 0.259 moles of calcium sulfate.

We are asked to find the volume to have 4.45g, let's see how many moles are equivalent. To do this we divide the required weight by the molecular weight (MW) of calcium sulfate.

MW of calcium sulfate = 136.1 g/mol

`\begin{gathered} \text{Mol of calcium sulfate }=\frac{\text{Mass of sample, g}}{MW,\text{ g/mol}} \\ \text{Mol of calcium sulfate = }\frac{4.45\text{ g}}{1361.1\text{ g/mol}}=0.03\text{ mol of calcium sulfate} \end{gathered}`

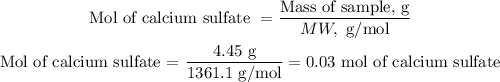
Now we apply a rule of three to know the required volume. In the same operation, we can make the conversion from liters to milliliters, since the answer is asked in milliliters.

`\begin{gathered} \frac{0.259\text{ mol}}{1L}=\frac{0.03\text{mol}}{x\text{ L}} \\ \text{Clear }x, \\ x=\frac{0.03\text{mol}*1L}{0.259\text{ mol}}*(1000mL)/(1L)=126.24\text{ mL} \end{gathered}`

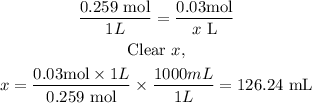
So, we will need 126.24 mL to supply 4.45 g from a 0.259M calcium sulfate solution