Question

Select all of the following points that lie on the graph of f(x) = 7 - 3x.

(-2, 1)
(-1, 10)
(0, 7)
(1, 5)
(2, 1)

Answer 1

So the person above me got it right (I think) but im small brain and dont wanna read all that so for all the ppl like me the answer is

(-1, 10)

(0, 7)

(2, 1).

Your welcome fellow lazy ppls :3

Answer 2

We know that

if the point belongs to the graph, then it must satisfy the given function.

We proceed to verify each of the points

we have

`f(x) = 7 - 3x`

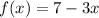
case a)
`(-2, 1)`

`x=-2\\y=1`

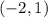
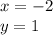
Substitute the value of x in the given function and compare the value of f(x) with the value of the coordinate y of the point

`f(x) = 7 - 3*(-2)`

`f(x) = 13`

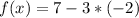
`13\\eq 1` --------> the point not lie on the graph

case b)
`(-1, 10)`

`x=-1\\y=10`

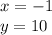
Substitute the value of x in the given function and compare the value of f(x) with the value of the coordinate y of the point

`f(x) = 7 - 3*(-1)`

`f(x) = 10`

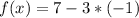
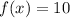
`10=10` --------> the point lie on the graph

case c)
`(0, 7)`

`x=0\\y=7`

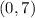
Substitute the value of x in the given function and compare the value of f(x) with the value of the coordinate y of the point

`f(x) = 7 - 3*(0)`

`f(x) = 7`

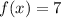
`7=7` --------> the point lie on the graph

case d)
`(1, 5)`

`x=1\\y=5`

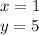
Substitute the value of x in the given function and compare the value of f(x) with the value of the coordinate y of the point

`f(x) = 7 - 3*(1)`

`f(x) = 4`

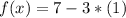
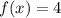
`4\\eq 5` --------> the point not lie on the graph

case e)
`(2, 1)`

`x=2\\y=1`

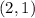
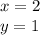
Substitute the value of x in the given function and compare the value of f(x) with the value of the coordinate y of the point

`f(x) = 7 - 3*(2)`

`f(x) = 1`

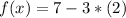
`1=1` --------> the point lie on the graph

therefore

the answer is

Points that lie on the graph are

`(-1, 10)`

`(0, 7)`

`(2, 1)`

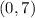
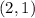
see the attached figure to better understand the problem