Question

Find the remainder when f(x) is divided by (x - k)
f(x) = 5x4 + 8x3 + 4x2 - 5x + 67; k = 2

Answer 1

It is to be solved by reminder thorem
f(x)/(x-k) will have reminder f(k),
so, f(2) = 5*(2^4) + 8 *(2^3) +4* (2^2) -5(2) +67

=5*16 + 8*8 +4*4 -5*2 +67
=80 + 64 + 16 -10 +67

= 217

Answer 2

Answer: The remainder when f(x) is divided by (x-2) is 217.

Explanation:

Since we have given that

`f(x) = 5x^4 + 8x^3 + 4x^2 - 5x + 67`

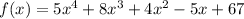
And it is divided by g(x)=(x-k)

Here, k= 2

So, g(x)= x-2

So, we need to find the remainder .

By using "Remainder theorem ":

`Put\ g(x)=0\\\\x-2=0\\\\x=2`

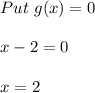
Now,

`f(2)=5(2)^4 + 8(2)^3 + 4(2)^2 - 5(2) + 67\\\\f(2)=80+64+16-10+67\\\\f(2)=217`

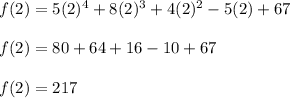
Hence, the remainder when f(x) is divided by (x-2) is 217.