Question

A pharmacy claims that the average medication costs $32 but it could differ as much as $8. Write and solve an absolute value inequality to determine the range of medication costs at this pharmacy.

A) |x − 32| ≥ 8; The medication costs range from $24 to $40
B)|x − 32| ≥ 8; The medications cost less than $24 or greater than $40.
C) |x − 32| ≤ 8; The medication costs range from $24 to $40
D) |x − 32| ≤8; The medications cost less than $24 or greater than $40.

Answer 1

So,

We can tell that the most expensive medication costs $40 and the cheapest costs $24. Thus, only options A and C are left.

To see which inequality is true, test a value, such as $30, in the equation in option C.

|30 - 32| ≤ 8
|-2| ≤ 8
2 ≤ 8

Option C is correct.

Answer 2

Therefore, Option C is correct that is
`|x-32|\leq8|{\text{the medication costs range from $24to $40}`.

Explanation:

We have given medication cost $32

Since, we have given as much as 8 so the inequality will maximum goes upto 8.

`|x-32|\leq8`

Now, we will solve the inequality for x we will get

We will first open the modulus function by its definition we will get

which is |x| is +x and -x

`(x-32)\leq8`

`x=32+8=40`

`x=40`

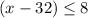
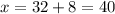
And
`-(x-32)\leq8`

`-x+32=8`

`x=24`

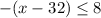
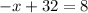
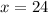
Therefore, Option C is correct