ANSWER
The solutions to this equation are: x = -2, x = -4 and x = -5
Step-by-step explanation
If (x + 2) is a factor, then x = -2 is one of the solutions to the equation. To find the other solutions we can divide the polynomial by this factor to find a quadratic equation that can be easily solved:
This means that this polynomial can be written as:

Now we can solve this equation to find the other two solutions:
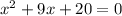
Using the following formula:
![\begin{gathered} ax^2+bx+c=0 \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/akuf1apf9if6mr85rckz.png)
For this problem:
![\begin{gathered} x=\frac{-9\pm\sqrt[]{9^2-4\cdot1\cdot20}}{2\cdot1} \\ x=\frac{-9\pm\sqrt[]{81-80}}{2} \\ x=(-9\pm1)/(2) \\ x_1=(-9+1)/(2)=(-8)/(2)=-4 \\ x_2=(-9-1)/(2)=(-10)/(2)=-5 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/gf17yi5u3w3taaqzj9nf.png)
So finally, the polynomial has 3 factors and can be written as:
