Question

Two point charges have a total electric potential energy of -24 J, and are separated by 29 cm.

If the total charge of the two charges is 45 μC, what is the charge, in μC, on the positive one?
What is the charge, in μC, on the negative one?

Answer 1

The charge of the negative one is 13.27 microcoulombs and the positive one has a charge of 58.27 microcoulombs.

Step-by-step explanation:

Electric potential energy between two point charges is derived from concept of Work, Work-Energy Theorem and Coulomb's Law and described by the following formula:

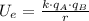`U_(e) = (k\cdot q_(A)\cdot q_(B))/(r)` (1)

Where:

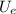`U_(e)` - Electric potential energy, measured in joules.

`q_(A)`,
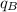`q_(B)` - Electric charges, measured in coulombs.

`r` - Distance between charges, measured in meters.

`k` - Coulomb's constant, measured in kilogram-cubic meters per square second-square coulomb.

If we know that
`U_(e) = -24\,J`,
`q_(A) = 45* 10^(-6)\,C+ q_(B)`,
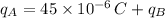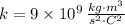`k = 9* 10^(9)\,(kg\cdot m^(3))/(s^(2)\cdot C^(2))` and
`r = 0.29\,m`, then the electric charge is:

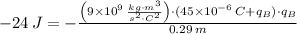
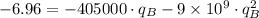
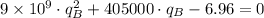`-24\,J = -(\left(9* 10^(9)\,(kg\cdot m^(3))/(s^(2)\cdot C^(2)) \right)\cdot (45* 10^(-6)\,C+q_(B))\cdot q_(B))/(0.29\,m)`

`-6.96 = -405000\cdot q_(B)-9* 10^(9)\cdot q_(B)^(2)`

`9* 10^(9)\cdot q_(B)^(2)+405000\cdot q_(B) -6.96 = 0` (2)

Roots of the polynomial are found by Quadratic Formula:

`q_(B,1) = 1.327* 10^(-5)\,C`,
`q_(B,2) \approx -5.827* 10^(-5)\,C`

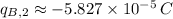
Only the first roots offer a solution that is physically reasonable. The charge of the negative one is 13.27 microcoulombs and the positive one has a charge of 58.27 microcoulombs.