Question

3) Wilbur's school is selling tickets to a choral performance. On the first day of ticket sales theschool sold 5 senior citizen tickets and 8 child tickets for a total of $103. The school took in $79on the second day by selling 5 senior citizen tickets and 4 child tickets. What is the price each ofone senior citizen ticket and one child ticket?

Answer 1

We have to find the price of one senior ticket and the the price of one child ticket.

We have to construct a system of equations from the information given and solve it.

Let S be the price of a senior ticket and C the price of a child ticket.

On the first day, they sold 5 senior tickets and 8 child tickets for $103.

This sales amount, $103, is the sum of the sales of senior tickets and the sales of child tickets.

The sum of senior tickets can be expressed as the number of tickets, which is 5, and the price of the senior ticket, which we don't know the value but we can express it as S. Then, the sales of senior tickets is 5*S.

The same can be said for child tickets, where the sales amount can be expressed as 8*C.

Then, we can write:

`5\cdot S+8\cdot C=103`

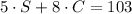
On the second day, they sold 5 senior tickets and 4 child tickets, totalling $79 in sales.

We can express this as:

`5\cdot S+4\cdot C=79`

Now we have a system of equations, with 2 equations and 2 unknowns:

`\begin{gathered} 5S+8C=103 \\ 5S+4C=79 \end{gathered}`

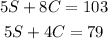
As we have 5S in both equations, we can solve for C with the elimination method: we will substract the second equation from the first.

`\begin{gathered} (5S+8C)-(5S+4C)=103-79 \\ 5S-5S+8C-4C=24 \\ 4C=24 \\ C=(24)/(4) \\ C=6 \end{gathered}`

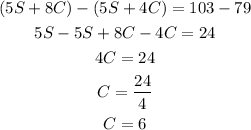
Knowing that C = 6, we can use any of the two equations and solve for S:

`\begin{gathered} 5S+8C=103 \\ 5S+8\cdot6=103 \\ 5S+48=103 \\ 5S=103-48 \\ 5S=55 \\ S=(55)/(5) \\ S=11 \end{gathered}`

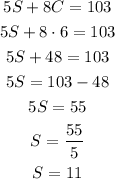
Answer: A senior citizen ticket costs $11 and a child ticket costs $6.