Question

Newton's law of cooling is T = Ae- + C, where Tis the temperature of the object at time, and is the constant temperature of the surrounding medium. Thetemperature of a cake is 360' when it is removed from the oven. The temperature in the room is 73'. In 12 minutes, the cake cools to 264'. How long will it take forthe cake to cool to 135? While solving this problem, round the value of k to seven decimal places. Round your answer to two decimal places.

Answer 1

To answer this question, first we have to find the values of A and k in the equation, to do it we can use some of the information given in the statement.

For example, to find A, we have to use the initial temperature of the cake, which is the value of T at t=0, and the temperature of the room:

`\begin{gathered} T=Ae^(-kt)+C \\ 360=Ae^(-k(0))+73 \\ 287=Ae^0 \\ 287=A \end{gathered}`

A has a value of 287.

To find the value of k, use the the temperature after 12 minutes, which is T when t=12, the value of A and the temperature of the room:

`\begin{gathered} 264=287e^(-k(12))+73 \\ 191=287e^(-12k) \\ (191)/(287)=e^(-12k) \\ ln((191)/(287))=-12k \\ k=(ln((191)/(287)))/(-12) \\ k=0.0339341 \end{gathered}`

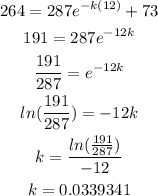
Now, that we know the values of A and k, we can find t when the temperature is 135:

`\begin{gathered} 135=287e^(-0.0339341t)+73 \\ 62=287e^(-0.0339341t) \\ (62)/(287)=e^(-0.0339341t) \\ ln((62)/(287))=-0.0339341t \\ t=(ln((62)/(287)))/(-0.0339341) \\ t=45.15 \end{gathered}`

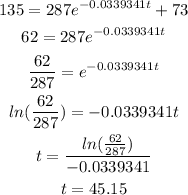
It means that it will take 45.15 minutes for the cake to cool to 135°.