Question

A marble is shot horizontally from a tabletop with an initial speed of 2.5 m/s using a marble launcher. Thetable is 0.8 meters high.a) what is the vxo of the marble?b) what is the vyo of the marble?c) what is the acceleration in the x-direction of the marble?d) what is the magnitude of the acceleration in the y-direction of the marble?e) how long does it take for the marble to hit the ground? (2 sig figs)f) how far will the marble travel along the floor before it lands? (2 sig figs)

Answer 1

Given,

The initial velocity of the projectile, v₀=2.5 m/s

The height of the table, y₀=0.8 m

As the marble was shot horizontally, the angle of the projection will be zero, i.e., θ=0°

a)The x-component of the initial velocity is given by,

`v_(0x)=v_0\cos \theta`

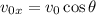
On substituting the known values,

`\begin{gathered} v_(0x)=2.5*\cos 0^(\circ) \\ =2.5\text{ m/s} \end{gathered}`

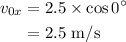
Thus the x-component of the velocity is 2.5 m/s

b) The y-component of the initial velocity is given by

`v_(0y)=v_0\sin \theta`

On substituting the known values,

`\begin{gathered} v_(0y)=2.5*\sin 0^(\circ) \\ =0\text{ m/s} \end{gathered}`

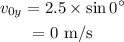
Thus the y-component of the velocity id 0 m/s

c) As there is no force acting in the x-direction the acceleration in that direction will be zero.

d) In the y-direction the gravity is acting on the marble throughout its flight. Thus the acceleration of the marble in y-direction will be equal to the acceleration due to gravity.

Thus the magnitude of the acceleration in the y-direction will be equal to 9.8 m/s²

e) Applying the equation of the motion in the y-direction,

`y=y_0+v_(0y)t+(1)/(2)gt^2`

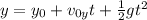
Where y is the final height of the marble, which is zero meters.

As we have taken height as positive, that is positive y-direction is upwards, the acceleration due to gravity will be negative, as its direction is downwards.

On substituting the known values in the above equation,

`\begin{gathered} 0=0.8+0+(1)/(2)*-9.8* t^2 \\ \Rightarrow t^2=(-0.8*2)/(-9.8) \\ \Rightarrow t^2=0.16 \\ \Rightarrow t=0.40\text{ s} \end{gathered}`

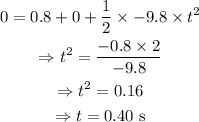
Therefore the time of flight is 0.40 s

f) The displacement of the marble in the x-direction, i.e., the length traveled by the marble along the floor is given by,

`x=v_(0x)t`

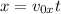
On substituting the values,

`\begin{gathered} x=2.5*0.4 \\ =1\text{ m} \end{gathered}`

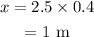
Therefore the distance traveled by the marble is 1 m