h is the height at time t
t is the time
v is initial vertical velocity
s is initial height
s = 68ft, v = 128ft/s
Therefore
h = -16t^2 + 128t + 68
The time the ball is in the air is the time it took the bullet to hit the ground (h = 0)
To find the time taken for the bullet to be in the air,
we set h = 0.
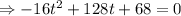
Dividing through by -16, we have;
![\begin{gathered} t^2-8t-(17)/(4)=0 \\ By\text{ completing the square method, we have} \\ (t-4)^2-(-4)^2-(17)/(4)=0 \\ (t-4)^2-(81)/(4)=0 \\ \Rightarrow t-4=\pm\sqrt[]{(81)/(4)} \\ \Rightarrow t=4\pm(9)/(2)=4-4.5\text{ or 4+4.5} \\ t=-0.5\text{ or 8.5} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/t3ahs6qoej7gbfyqn4yc.png)
Since t cannot be negative, then the only possibility is
t = 8.5s
Hence the bullet was in the air for 8.5s