Question

A factory produces 1,250,000 toys each year. The number of toys is expected to increase by about 150% per year. Which model can be used to find the number of toys being produced, n (in millions), in t years?

A. n= 2.5(1.5)/t, t cannot = 0
B. n= 1.5t^2 + 1.25
C. n= 1.5t + 1.25
D. n= 1.25(2.5^t)

Answer 1

The correct option is D.

Explanation:

It is given that the factory produces 1,250,000 toys each year.

In the function n (in millions), So the initial production is 1.25 million.

The increasing rate is 150%. THe increasing rate is 1.5.

The function is defined as,

`n=n_0(1+r)^t`

Where n₀ is initial production, r is rate and t is time.

`n=1.25(1+1.5)^t`

`n=1.25(2.5)^t`

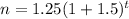
Therefore the correct option is D.

Answer 2

For this case we have a function of the form:

`image`

Where,

n0: initial amount (in units of millions)

b: growth rate

t: time in years

Substituting values we have:

`image`

Answer:

the number of toys being produced, n (in millions), in t years is:

D.
`n = 1.25 (2.5 ^ t)`