Question

Find the equation for the graph of the quadratic function below.

Answer 1

`f(x)=4(x-2)^2\text{ + 7}`

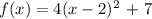
Step-by-step explanation:

The equation of quadratic function in vertex form is given by:

`\begin{gathered} f(x)=a(x-h)^2\text{ + k} \\ \\ \text{where vertex = (h, k)} \end{gathered}`

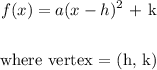
We need to et the vertex of the function from the graph. The tip of the parabola is at x = 2 and y = 7

The vertex is the tip of the parabola.

Vertex (h, k): (2, 7)

h = 2, k = 7

The equation of the quadratic function becomes:

`\begin{gathered} f(x)=a(x-2)^2\text{ + 7} \\ \\ To\text{ get a, we n}eed\text{ to pick another point on the graph} \\ U\sin g\text{ the point: (0, -1)} \end{gathered}`

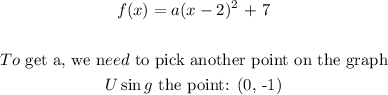
Substitute for x and f(x) in the function above:

`\begin{gathered} \text{where x = 0, f(x) = y = -1} \\ -1\text{ = a(0 - 2) + 7} \\ -1\text{ = a(-2) + 7} \\ -1\text{ = }-2a\text{ + 7} \\ -1\text{ - 7 = -2a} \\ -8\text{ = -2a} \\ a\text{ = -8/-2} \\ a\text{ = 4} \end{gathered}`

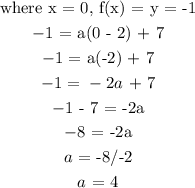
The equation of the quadratic function:

`f(x)=4(x-2)^2\text{ + 7}`