Question

What is the solution of log3x − 5 16 = 2?

the base is 3x - 5, and the argument is 16

Answer 1

Hello,

log (16)=2 in base 3x-5
==>16=2^(3x-5)
==>2^4=2^(3x-5)
==>4=3x-5
==>3x=9
==>x=3

Answer 2

x=3

Explanation:

The given equation is
`\log_(3x-5)16=2`

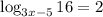
The relation between logarithmic function and exponential function is given by

`\text{If }y=b^x\text{ then }x=\log_b(y)`

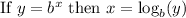
On comparing, we get

b = 3x-5

y = 16

x = 2

Hence, using the relation, we have

`16=(3x-5)^2`

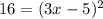
Take square root both sides

`\pm√(16)=3x-5`

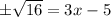
On simplifying

`3x-5=\pm4\\\\3x=\pm4+5\\\\x=(1)/(3)(5\pm4)\\\\x=(1)/(3)*1,(1)/(3)*9\\\\x=(1)/(3),3`

For x = 1/3

`3x-5\\\\=3\cdot (1)/(3)-5\\\\=-4`

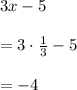
Base cannot be negative.

Hence, the value of x is 3