Question

The volumes of two similar solids are 1,728 m^3 and 343 m^3. The surface area of the larger solid is 576 m^2. What is the surface area of the smaller solid? a. 196 m^2 b. 76m^2 c. 1,372m^2 d. 392 m^2

Answer 1

Scale factor = (1728/343)^(1/3) = 12/7 Let the surface area of the smaller solid be A, then: A * (12/7)^2 = 576 So A = 196

Answer 2

Option a. 196 m²

Explanation:

Volumes of two similar solids are 1728 m³ and 343 m³

So the ratio of these volumes =
`(343)/(1728)`

Now we know volume is a three dimensional unit so we find the cube root of the ratio of the volumes to find the ratio of sides.

Scale factor =
`\sqrt[3]{(343)/(1728) }=(7)/(12)`

Now we know area of solids is a two dimensional unit so we will square the scale factor and this will be the ratio of area

(Scale factor)² =
`((7)/(12))^(2)` = (Surface area of smaller solid)/(surface area of larger solid)

Area of larger solid = 576 m²

`((7)/(12))^(2)=(S)/(576)`

`S=(49)/(144).(576)=(49).(4)=196`

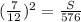
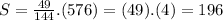
Surface area of of the smaller solid = 196 m²

Option A. is the answer.