Answer:
C.
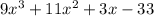
Explanation:
A polynomial is prime if it can't be factored in polynomials of lower degree. Let's factorize:
A.
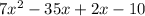
In this case we have 4 terms, so we can use Grouping:
Part a:
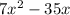
We're going to use Greatest common factor:

Part b:

In this part we also use greatest common factor:
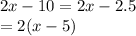
Then,
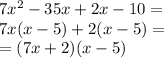
This polynomial is not prime.
B.

This polynomial cannot be factorized then it's prime.
C.
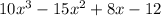
In this polynomial we can use grouping too:
Part a:

Part b:
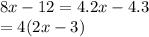
Then,
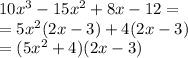
This polynomial isn't prime.
D.
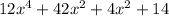
First we're going to use Greatest common factor:
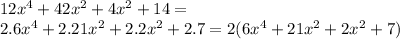
Now we're going to apply grouping on the terms inside of the parenthesis:
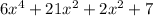
Part a:

Part b:
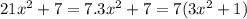
Then,
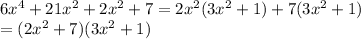
Remember that at the beginning we use Greatest common factor:
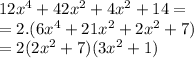
This polynomial isn't prime.