Let's fist talk about the sine and cosine function. We know that both functions are periodic with period 2pi, that is:
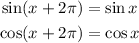
We also know that both functions are bounded in the intervale [-1,1], which means that:
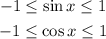
Both the sine and cosine functions have defined parity, the sine function is odd and the cosine function is even, that is:
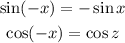
Now, let's talk about the remaining trigonometric functions. They are defined as:
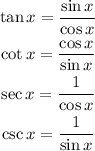
Since this four functions are defined from the sine and cosine function they will inherite some properties from this functions. The tangent, cotangent, secant and cosecant are all periodic functions; the first two have a period of pi and the reamining two have a period of 2pi, then we have:
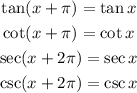
They also have defined parity. The secant is even and the remaining three functions are odd, that is:
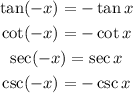
One property that this functions don't inherite is that they are not bounded functions.
Let's sum up what we learn so far.
Similarities:
All the trigonometric functions are periodic and have defined parity.
Differences:
The sine and cosine functions are bounded while the reamining functions are unbounded.