Question

1. **A volleyball is hit upward by a player in a game. The height h (in feet) of the volleyball after t seconds is given by g = -8t^2 + 32 +6.

Answer 1

`g=-8t^2+32t+6`

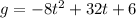
B.

This equation represent the position of the ball if we derivate we find the speed

`\begin{gathered} -8(2)t+32(1)+0 \\ s=-16t+32 \end{gathered}`

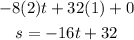
we replace the speed by 0 to solve t, the value of t will be seconds when the heigth is maximum

`\begin{gathered} 0=-16t+32 \\ 16t=32 \\ t=(32)/(16) \\ \\ t=2 \end{gathered}`

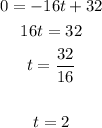
After 2 seconds the heigth is maximum

C.

We replace a heigth 0 on the first equation to find when the ball hit the ground

`0=-8t^2+35t+6`

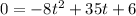
it is a polynomial then we can use quatratic formula to solve

`-8t^2+35t+6=0`

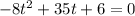
where -8 is a, 35 is b and 6 c

`t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

replacing

`t=\frac{-(35)\pm\sqrt[]{(35)^2-4(-8)(6)}}{2(-8)}`

simplify

`\begin{gathered} t=\frac{-35\pm\sqrt[]{1225+192}}{-16} \\ \\ t=\frac{-35\pm\sqrt[]{1417}}{-16} \\ \\ t=(-35\pm37.6)/(-16) \end{gathered}`

we obtan to values for t

`\begin{gathered} t_1=(-35+37.6)/(-16)=-0.1625 \\ \\ t_2=(-35-37.6)/(-16)=4.5375 \end{gathered}`

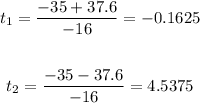
we chose the second value because the time cant be negative

then time when the ball hit the ground is 4.54 seconds