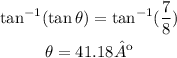The distance between the base of the elevator and the grain bin, the height of the grain bin, and the distance between the elevator and the distance between the elevator and the top of the grain bin form a right triangle.
To determine the slope of the elevator (marked in the sketch with x) you can use the Pythagorean theorem, which states that the square of the hypothenuse is equal to the sum of the squares of the legs of the triangle:
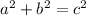
Where
a and b represent the legs of the triangle
c represents the hypothenuse
For our triangle:
a= 32ft
b= 28ft
c= x
![\begin{gathered} 32^2+28^2=x^2 \\ 1024+784=x^2 \\ 1808=x^2 \\ \sqrt[]{1808}=\sqrt[]{x^2} \\ x=4\sqrt[]{113}ft \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/3954ulvbjskc9g04o3ly.png)
Next, to determine the angle of elevation (marked on the sketch with yº) you can use trigonometric ratios. In this case, given that we know the lengths of the side across the angle and the side next to the angle. The trigonometric ratio that relates both sides is the tangent defined as follows:
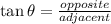
Where
θ represents the angle of interest
opposite refers to the side across the angle
adjacent refers to the side next to the angle
So, the tangent of the angle of elevation can be expressed as:
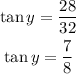
Apply the inverse tangent to both sides of the equal sign to determine the measure of the angle: