Question

Find the area of the shaded sector of the circle 28m and 140 degrees

Answer 1

The shaded portion is a minor sector with diameter = 28m

therefore,

Radius ,r = diameter/2

Radius, r=28m/2=14m

Next, we have to calculate the angle of the sector

The angle of the sector is connected to the 140° on a straight line

Let the angle of the sector be

`\phi`

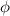
Therefore,

`\begin{gathered} \phi+140^0=180^0 \\ \phi=180^0-140^0 \\ \phi=40^0 \end{gathered}`

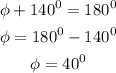
Then we can calculate the area of a sector using the formula

`\begin{gathered} \text{Angle of sector=}(\phi)/(360)*\pi r^2 \\ \text{Where,} \\ r=14m \\ \phi=40^0 \\ \pi=3.14(\text{ but the answer has to be in terms of }\pi) \end{gathered}`

On substitution, we will have the area of the sector as

`\begin{gathered} \text{Area of shaded sector}=(40)/(360)\pi*14^2 \\ \text{Area of shaded sector=}21.78\pi m^2 \\ \text{Area of shaded sector=21.78}\pi\text{m}^2 \end{gathered}`

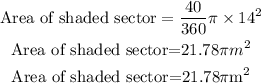
Therefore,

The area of the shaded sector in terms of π = 21.78πm²