Question

The teacher separated her class of twenty-eight students in two groups. One group has 4 more than twice as many students as thw ither group. How many students are in each group?

PLEASE SHOW WORK

Answer 1

`a+b=28 \\\\\ a=2b+4 \\\\ 2b+4+b=28\\\\ 3b=28-4\\\\3b=24 \\\\ \boxed{b=(24)/(3)=8} \\\\a=2*8+4\\\\a=16+4 \\\\ \boxed{a=20}`

Answer 2

Let x be the first group of students in a class and y be the second group of students in the class.

As per the statement:

As, the teacher separated her class of twenty-eight students in two groups.

⇒ x+y = 28 ......[1]

Also, one group has 4 more than twice as many as the other group.

⇒ x = 4 + 2y ......[2]

Now, substitute the equation [2] in [1]; we have

`4+2y+y = 28`

Combine like terms;

4 + 3y = 28

Subtract 4 from both sides we get;

`4+3y-4 = 28-4`

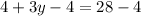
Simplify:

3y = 24

Divide by 3 to both sides we get;

`(3y)/(3) = (24)/(3)`

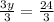
Simplify:

y = 8

Now, substitute the value of y in equation [2] to solve for x;

`x = 4 + 2(8) = 4 +16 = 20`

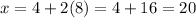
or

x = 20

therefore, the number of students in each group are 20 and 8.