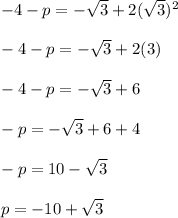Question

Please solve as soon as possible. lf a line makes an angle of tan^-1(-1/√3) with x axis and passes through the points (-p, -2√3) and (4, -1) find the value of p.​

Answer 1

Answer:
`p = -10+√(3)`

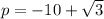
When writing this on a keyboard, we could say p = -10+sqrt(3)

===========================================================

Step-by-step explanation:

We're told the angle between the line and x axis is
`\tan^(-1)\left((-1)/(√(3))\right)`

This is one of the infinitely many exact solutions to the equation
`\tan(\theta) = (-1)/(√(3))` where
`\theta` (Greek letter theta) is the angle in question.

It turns out that the tangent ratio is exactly the slope of a line.

• slope = rise/run
• tan(angle) = opposite/adjacent

Both describe a ratio of how far something moves up or down, over how far it moves to the right.

So saying
`\tan(\theta) = (-1)/(√(3))` means that the slope of our mystery line is exactly
`(-1)/(√(3))`

-------------------------------

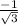
What we'll do is compute the slope on the points
`(\ -p, -2√(3) \ ) \text{ and } (4, -1)`

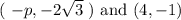
That produces some algebraic expression in terms of p. That expression is set equal to the previously mentioned slope of
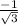`(-1)/(√(3))` which will allow us to solve for p.

Part 1

`m = \text{slope}\\\\m = (y_2-y_1)/(x_2-x_1)\\\\m = (-1-(-2√(3)))/(4-(-p))\\\\m = (-1+2√(3))/(4+p)\\\\-(1)/(√(3)) = (-1+2√(3))/(4+p) \ \ \text{ ... plug in the previously mentioned slope}\\\\-(4+p) = (√(3))(-1+2√(3)) \ \ \text{ ... cross multiply}\\\\`

Part 2

`-4-p = -√(3)+2(√(3))^2\\\\-4-p = -√(3)+2(3)\\\\-4-p = -√(3)+6\\\\-p = -√(3)+6+4\\\\-p = 10-√(3)\\\\p = -10+√(3)\\\\`