Question

Ap calculus, please help me, i dont understand

Answer 1

`\displaystyle y = Ce^\bigg{(x^2)/(2)} - 1`

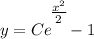
General Formulas and Concepts:

Pre-Algebra

• Equality Properties

Algebra I

• Functions
• Function Notation
• Exponential Rule [Multiplying]:
  `\displaystyle b^m \cdot b^n = b^(m + n)`

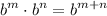
Algebra II

• Natural Logarithms ln and Euler's number e

Calculus

Derivatives

Derivative Notation

Basic Power Rule:

• f(x) = cxⁿ
• f’(x) = c·nxⁿ⁻¹

Slope Fields

• Solving differentials
• Separation of Variables

Antiderivatives - Integrals

Integration Constant C

Integration Rule [Reverse Power Rule]:
`\displaystyle \int {x^n} \, dx = (x^(n + 1))/(n + 1) + C`

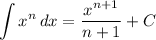
U-Substitution

Logarithmic Integration:
`\displaystyle \int {(1)/(x)} \, dx = ln|x| + C`

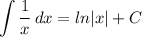
Explanation:

Step 1: Define

`\displaystyle y' = x(1 + y)`

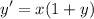
Step 2: Redefine

Separation of Variables. Get differential equation to a form where we can integrate both sides.

1. [Division Property of Equality] Isolate x:
   `\displaystyle (1)/(1 + y)y' = x`
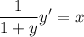
2. Rewrite derivative notation:
   `\displaystyle (1)/(1 + y) \ (dy)/(dx) = x`
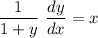
3. Rewrite:
   `\displaystyle (1)/(1 + y) \ dy = x \ dx`

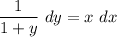
Step 3: Find General Solution Pt. 1

1. [Equality Property] Integrate both sides:
   `\displaystyle \int {(1)/(1 + y)} \, dy = \int {x} \, dx`
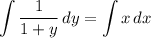
2. [Right Integral] Integrate [Integration Rule - Reverse Power Rule]:
   `\displaystyle \int {(1)/(1 + y)} \, dy = (x^2)/(2) + C`

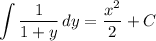
Step 4: Find General Solution Pt. 2

Identify variables for u-substitution.

1. Set:
   `\displaystyle u = 1 + y`
2. Differentiate [Basic Power Rule]:
   `\displaystyle du = dy`

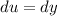
Step 5: Find General Solution Pt. 3

1. [Integral] U-Substitution:
   `\displaystyle \int {(1)/(u)} \, du = (x^2)/(2) + C`
2. [Integral] Integrate [Logarithmic Integration]:
   `\displaystyle ln|u| = (x^2)/(2) + C`
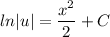
3. Back-Substitute:
   `\displaystyle ln|1 + y| = (x^2)/(2) + C`
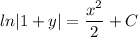
4. [Equality Property] e both sides:
   `\displaystyle e^\bigg1 + y = e^\bigg{(x^2)/(2) + C}`
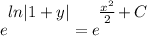
5. Simplify:
   `\displaystyle |1 + y| = e^\bigg{(x^2)/(2) + C}`
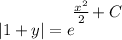
6. Rewrite:
   `\displaystyle |1 + y| = Ce^\bigg{(x^2)/(2)}`
7. Rewrite:
   `\displaystyle 1 + y = \pm Ce^\bigg{(x^2)/(2)}`
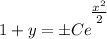
8. [Subtraction Property of Equality] Isolate y:
   `\displaystyle y = \pm Ce^\bigg{(x^2)/(2)} - 1`

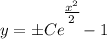
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Slope Fields

Book: College Calculus 10e