SOLUTION
The number of diagonals and number of sides of a polygon are related with the formula
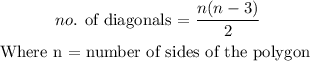
Substituting we have
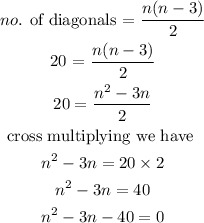
Solving the quadratic equation for n, we have
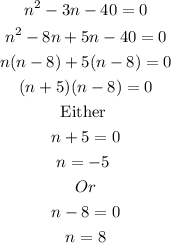
So, we will go with n = 8, since the number of sides cannot be a negative number.
Now, sum of interior angles in a regular polygon is given by
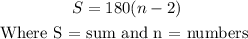
So we have
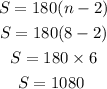
So, the measure of an interior angle becomes
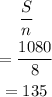
Hence the answer is 135 degrees