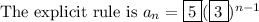9514 1404 393
Answer:
recursive: 5, 3, 2
explicit: 5, 3
Explanation:
First of all, you can identify the first term as a1 = 5.
Then you can see that the ratio of consecutive terms is ...
15/5 = 45/15 = 135/45 = 405/135 = 3 . . . the common ratio
In the recursive formula, a1 is the first term (5), and the multiplier getting you to the next term is the common ratio (3). The recursion relation is good for values of n such that n-1 is at least 1. That is, n ≥ 2.
__
The explicit rule is formed the way the problem statement tells you: the first term times a power of the common ratio.