Answer:
First term is 5
Fourth term is 5.5
Tenth term is 6.5
Explanation:
Given :The rule as
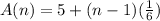
We have to find find the first,fourth,and tenth terms of the arithmetic sequence.
Consider the given rule ,
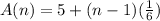
For first term , put n = 1
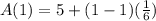
Simplify , we have,

For fourth term, Put n = 4
we have,
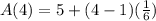
Simplify, we have,

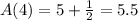
For tenth term, put n = 10 ,
We have,
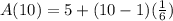
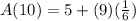
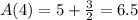
Thus, First term is 5
Fourth term is 5.5
Tenth term is 6.5