Question

At a concession stand, three hot dogs and four hamburgers cost $ 14.25 and four hamburgers and three hot dogs cost $13.75. Find the cost of one hamburger and one hot dog.

Answer 1

I commented on your question but I'll solve it as if the second scenario had 4 hot dogs and 3 hamburgers totaling $13.75

Let D represent hot dogs. Let H represent hamburgers.


`3D+4H=14.25\\ 4D+3H=13.75`

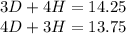
This is called a system of equations. You must substitute one equation into the other. I'll work it through, and hopefully you can follow along.


`3D+4H=14.25\\ 3D+4H-4H=14.25-4H\\ 3D=14.25-4H\\ (3D)/(3)=(14.25)/(3)-(4H)/(3)\\ D=(19)/(4)-(4)/(3)H`

Now you have the value of one hot dog (D). Substitute this value into the other equation. This way you will only be working with the H variable.


`4D+3H=13.75\\ 4((19)/(4)-(4)/(3)H)+3H=13.75\\ 19-(16)/(3)H+3H=13.75\\ -(16)/(3)H+3H=13.75-19\\ -(7)/(3)H=-(21)/(4)\\ -(7)/(3)H*(3)/(7)=-(21)/(4)*(3)/(7)\\ -1H=-(9)/(4)\\ H=(9)/(4)`

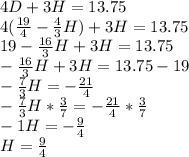
9/4=2.25 for the price of a Hamburger (H).
Now plug the value for H (2.25) into either equation.


`3D+4H=14.25\\ 3D+4(2.25)=14.25\\ 3D+9=14.25\\ 3D=5.25\\ D=1.75`

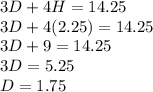
The price for a Hamburger is $2.25
The price for a Hot Dog is $1.75