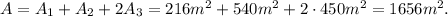Answer:
The surface area of the prism is
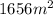 .
.
Explanation:
In order to obtain the surface area we need to find the areas of all the sides. Then, we have two triangles and three rectangles.
Let us find the area of the triangles and denote it by
 . Notice that both triangles are equal. We know that the area of a triangle is
. Notice that both triangles are equal. We know that the area of a triangle is
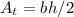
where
 stands for the length of the base, and
stands for the length of the base, and
 stands for the length of the height. From the figure we know that
stands for the length of the height. From the figure we know that
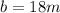 and
and
 . Hence, the area of the triangle is
. Hence, the area of the triangle is
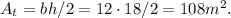
To obtain the area of both sides we only need to multiply
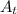 by two:
by two:
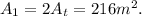
Let us find now the area of the bottom rectangle and denote by
 . The area of the rectangle is
. The area of the rectangle is
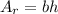 , where
, where
 stands for the length of the base, and
stands for the length of the base, and
 stands for the length of the height. From the figure we know
stands for the length of the height. From the figure we know
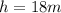 and
and
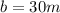 . So,
. So,
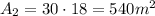 .
.
For the other two rectangle notice that they have the same dimensions: the length of the base is 30m and the length of the height is 15. So, the area of one of them is
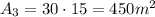 .
.
Finally, the surface area is the result of adding all the areas: