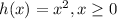Question

If h is the function given by h(x) = (f•g)(x) where f(x) =(sqrtx)^3, then h(x) =

Answer 1

We have the following functions

`\begin{gathered} f(x)=\sqrt[]{x}=x^{(1)/(2)} \\ g(x)=(\sqrt[]{x})^3=x^{(3)/(2)} \end{gathered}`

We want to find:

`h(x)=(fg)(x)=f(x)* g(x)`

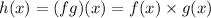
If we substitute and do the product:

`f(x)* g(x)=x^(1/2)* x^(3/2)=x^((1/2+3/2))=x^(4/2)=x^2`

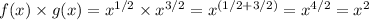
Our h(x) function is:

`h(x)=x^2`

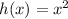
We still need to be careful about the domain. The restrictions from the f(x) and g(x) function remains, then the function h(x) will be defined only for

x >= 0.

`h(x)=x^2,x\ge0`