Answer:
The coordinates of the point 3/5 of the way from A(-4,-4) to B(6,6) are (2, 2).
Explanation:
Given the points
We need to find the coordinates of the point 3/5 of the way from A(-4,-4) to B(6,6).
Let P be the required point, then
AP : AB = 3 : 5
as
so
AP / AB = 3/5
AP / (AP + BP) = 3/5
5AP = 3(AP + BP)
5AP = 3AP + 3BP
2AP = 3BP
AP/BP = 3/2
AP : BP = 3 : 2
The formula of the coordinates of a point that divides the line joining the points (a, b) and (c, d) in the ratio m : n is:

For the given division,
m : n = 3 : 2
Thus, the coordinates of the point P are:

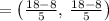
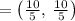
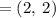
Therefore, the coordinates of the point 3/5 of the way from A(-4,-4) to B(6,6) are (2, 2).