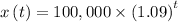Question

A social media website had 100,000 followers its first year. The number of followers increased by 9% each year. Write an exponential growth function to represent this situation

Answer 1

an exponential growth function to represent this situation is:

`x\left(t\right)=100,000* \left(1.09\right)^t\:`

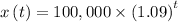
Explanation:

We know that the exponential growth function is of the form

`x\left(t\right)\:=\:x_0\:* \:\left(1\:+\:r\right)^t`

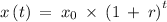
where

• x(t) represents the value at time t

• x₀ represents the initial value at time t = 0. In other words, it is the initial value (the amount before measuring growth or decay)

• r represents the growth factor when r > 0 and decay factor when r < 0

• t represents the of time intervals that have passed

In our case,

Given that

A social media website had 100,000 followers its first year. Thus,

• x₀ = 100,000

The number of followers increased by 9% each year. Thus,

• r = 9% = 0.09

Thus, substituting r = 0.09 and x₀ = 100,000 in the growth function

`x\left(t\right)\:=\:x_0\:* \:\left(1\:+\:r\right)^t`

`x\left(t\right)=100,000* \left(1+0.09\right)^t\:`

`x\left(t\right)=100,000* \left(1.09\right)^t\:`

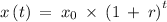
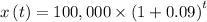
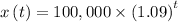
Therefore, an exponential growth function to represent this situation is:

`x\left(t\right)=100,000* \left(1.09\right)^t\:`