Question

Please helppp, I'm using all my points!! Line A passes through the points (-3,-4) and (-6,-5). Write the equation of the image of A after a dilation with a scale factor of 2. Write your in answer in slope-intercept form.

y=

Answer 1

The equation of the image of A after a dilation with a scale factor of 2 will be:

• 
  `y\:=\:(1)/(3)x\:-6`

Explanation:

Some background Knowledge about dilation.

We know that when an object is dilated by a scale factor, it gets reduced, stretched, or remains the same, depending upon the value of the scale factor.

• If the scale factor > 1, the image is enlarged

• If the scale factor is between 0 and 1, it gets shrunk

• If the scale factor = 1, the object and the image are congruent

Rule to calculate the dilation by a scale factor 2 centered at the origin

P(x, y) → P'(2x, 2y)

Here, P'(2x, 2y) is the image of P(x, y).

• It means the coordinates of the image can be determined by multiplying the coordinates of the original point by 2.

Now, let us solve our case:

Given the points

• (-3, -4)

• (-6, -5)

Let say the points are X(-3, -4) and Y(-6, -5)

Rule to calculate the dilation by a scale factor 2 centered at the origin

P(x, y) → P'(2x, 2y)

so

X(-3, -4) → X' (2(-3), 2(-4)) → X'(-6, -8)

Y(-6, -5) → Y' (2(-6), 2(-5)) → Y'(-12, -10)

Thus, after the dilation scale of factor 2, now the image line will through the points X'(-6, -8) and Y'(-12, -10)

so we have the points of the image line

• X'(-6, -8)

• Y'(-12, -10)

Determining the slope between X'(-6, -8) and Y'(-12, -10)

`\left(x_1,\:y_1\right)=\left(-6,\:-8\right),\:\left(x_2,\:y_2\right)=\left(-12,\:-10\right)`

`m=(-10-\left(-8\right))/(-12-\left(-6\right))`

`m=(1)/(3)`

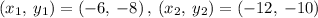
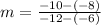
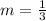
The slope-intercept form of the line equation

y = mx+b

where

• m is the slope

• b is the y-intercept

now substituting m = 1/3 and (-6, -8) in the slope-intercept form of the line equation

`y = mx + b`

`-8\:=\:(1)/(3)\left(-6\right)\:+\:b`

`-2+b=-8`

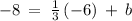
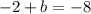
Add 3 to both sides

`-2+b+2=-8+2`

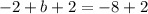
Simplify

`b=-6`

now substituting b = -6 and m = 1/3 in the slope-intercept form of line equation

`y = mx + b`

`y\:=\:(1)/(3)x\:+\:\left(-6\right)`

`y\:=\:(1)/(3)x\:-6`

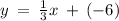
Therefore, the equation of the image of A after a dilation with a scale factor of 2 will be:

• 
  `y\:=\:(1)/(3)x\:-6`