Question

what is the measure of the radius, c, rounded to the nearest hundredth? use an appropriate trigonometric ratio to solve.

Answer 1

To find the central angle of a polygon we just divide 360° by the number of sides that the polygon has, in this case, we have a pentagon, then the central angle of the polygon is:

`CA=(360)/(5)=72`

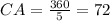
In the figure this angle is represented like this:

If we bisect this angle, which is dividing it by 2, we get the angle θ:

`\theta=(72)/(2)=36`

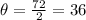
We know that the cosine of the angle θ is:

`\cos (\theta)=(10)/(c)`

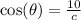
By solving for c from this ratio we get:

`\begin{gathered} \cos (\theta)=(10)/(c) \\ c*\cos (\theta)=(10)/(c)* c \\ c*\cos (\theta)=10*(c)/(c) \\ c*\cos (\theta)=10 \\ (c*\cos (\theta))/(\cos (\theta))=(10)/(\cos (\theta)) \\ c*(\cos (\theta))/(\cos (\theta))=(10)/(\cos (\theta)) \\ c=(10)/(\cos (\theta))=(10)/(\cos (36))\approx12.36\text{ cm} \end{gathered}`

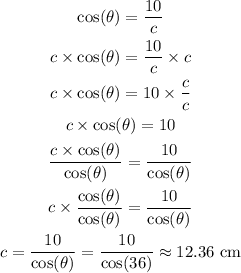
Then, the measure of the radius equals 12.36 cm