Question

The number of widgets that a manufacturing plant can produce varies jointly as the number of workers and the time they have worked.1. Find the constant of proportionality, K, to 2 decimal places, if 445 workers work 19 hours and can produce 81675.3 widgets.k =2. How many widgets (nearest tenth) can be produced by 495 workers in 30 hours?Widgets =

Answer 1

`\begin{gathered} 1)\text{ }k=9.66 \\ \\ 2)\text{ }143,451.0\text{ widgets} \end{gathered}`

Step-by-step explanation

1. Let the number of widgets be N.

Let the number of workers be n.

Let the time they have worked be t.

The number of widgets varies jointly as the number of workers and the time they have worked. This implies that:

`\begin{gathered} N\propto nt \\ \\ N=knt \end{gathered}`

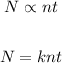
where k = constant of proportionality

To find the value of k, substitute the given values into the equation above and solve for k:

`\begin{gathered} 81675.3=k*445*19 \\ \\ 81675.3=k*8455 \\ \\ k=(81675.3)/(8455) \\ \\ k=9.66 \end{gathered}`

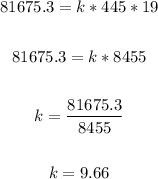
That is the constant of proportionality.

2. To find the number of widgets produced, substitute the constant of proportionality, number of workers, and the time into the formula for the number of widgets and simplify:

`\begin{gathered} N=9.66*495*30 \\ \\ N=143,451.0\text{ widgets} \end{gathered}`

That is the number of widgets.