Question

The distance y in miles) that Train A travels in x hours is represented by the equation y= 72x is train A or train B faster ?

Answer 1

The speed of Train A = 72 miles per hour

The speed of Train B = 68 miles per hour

Therefore, Train A runs faster because the speed of train A is greater than the speed of train B.

Hence, Train A is faster than Train B

Explanation:

The slope-intercept form of the line equation

`y = mx+b`

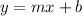
where

• m is the rate of change or slope

• b is the y-intercept

Train A)

The distance y (in miles) that Train A travels in x hours is represented by the equation:

y = 72x

comparing with the slope-intercept form of the linear/line equation

So, the rate of change or slope of Train A is: m = 72

• As the slope represents the speed of the train.

Therefore, the speed of Train A = 72 miles per hour

Train B)

Taking two points from the given graph of Train B

• (1, 68)

• (2, 136)

Determining the slope between (1, 68) and (2, 136)

(x₁, y₁) = (1, 68)

(x₂, y₂) = (2, 136)

Using the formula

Slope = m = [y₂ - y₁] / [x₂ - x₁]

= [136 - 68] / [2 - 1]

= 68 / 1

= 68

So, the rate of change or the slope of the line = m = 68

• As the slope represents the speed of the train.

Therefore, the speed of Train B = 68 miles per hour

Conclusion:

As

The speed of Train A = 72 miles per hour

The speed of Train B = 68 miles per hour

Therefore, Train A runs faster because the speed of train A is greater than the speed of train B.

Hence, Train A is faster than Train B