Answer: 6.72 seconds
This value is approximate.
===========================================================
Step-by-step explanation:
You are correct in noticing that h = 0 corresponds when the rocket is on the ground.
Plug this h value into the equation to get

You'll need the quadratic formula to solve for t.
Plug in a = -16, b = 100, c = 50.
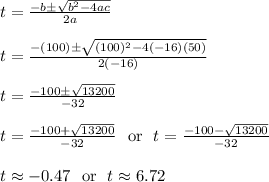
Ignore the negative solution because a negative time value does not make sense. The only reasonable solution is roughly t = 6.72
It takes approximately 6.72 seconds for the rocket to hit the ground.